A slide rule, one of the last vestiges of geek
nerddom in the fifties and sixties, is a remarkable invention.
Unfortunately, having been replaced by the electronic calculator, the slide
rule has fallen into disuse, which is a shame because it is an excellent conceptual
tool for visualizing how to do computations with logarithmic numbers.
The easiest way to explain how a normal
slide
rule works for multiplication and division of numbers is to illustrate first how two
linear rulers can be used for addition (or subtraction).
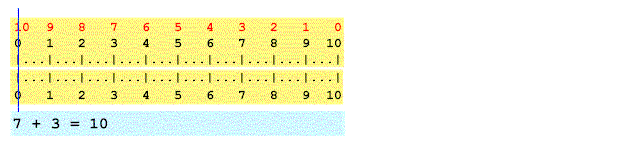
Hold the mouse pointer over the image below to
see how 7 + 3 are added with two linear rulers.
- The blue hairline is first
positioned over 7 on the
lower ruler.
- Next the upper ruler is moved
positioning its 0
over 7 on the lower
ruler.
- Then the blue hairline is moved over
3
on the upper ruler.
- Finally, the sum
= 10 is
read by noting the number on the lower ruler aligned with the blue hairline.
Now, hold the mouse pointer over the image below to
see how 15 + 5 are added with two linear rulers.
Note: The number 15 is not found on the ruler and so the two numbers
to be added are first divided
by 10 -- yielding 1.5 and 0.5
-- and their sum
is then multiplied by 10 to get the final answer.
- The blue hairline is first
positioned over 1.5 ( = 15 / 10) on the
lower ruler.
- Next the upper ruler is moved so
that 0 is
over 1.5 on the lower ruler.
- Then the blue hairline is
positioned over
0.5 ( = 5 / 10) on the upper
ruler.
- Finally, the "sum"
is read by noting the number, i.e., 2.0,
on the lower ruler aligned with the blue hairline; the true
sum = 2.0 x 10 = 20.
A slide rule
works by adding or subtracting the numerical exponents
of numbers for multiplication or division,
respectively.
- Thus, numbers to be multiplied or
divided are converted to their logarithmic values and their exponents are
added or subtracted.
- Then, the product or quotient is
found by taking the antilog of the resulting exponent.
- The beauty of a slide rule is that
the logarithmic conversions are automatically built into the
numerical scales of the slide rule as illustrated below by the two types of
number formats found on slide rule scales.
The beauty of a slide rule is that
the logarithmic conversions are automatically built into the
numerical scales of the slide rule as illustrated below by the two types of
number formats found on slide rule scales.
Slide Rule Number
Formats
Raw
Number Log Scale (base 10) |
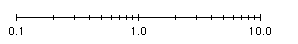 |
|
| Linear
Logarithmic
Scale (base 10) |
Here, the Raw Number Log Scale
is aligned with the Linear Logarithmic Scale of logarithmic
values (exponents of 10) that yield the corresponding raw numbers.
- For
example, 0.0 on the lower scale is the exponent of 10 that yields
the raw number,1.0 (1.0
= 100.0) on the upper scale.
- As another example, 1.0 one the
lower scale is the
exponent of 10 that yields the raw number 10 (10.0 = 101.0) on the
upper scale.
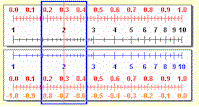
In order to see how a regular slide
rule is used to calculate products and ratios, click on slide
rule image below.
Interactive
Slide Rule
|