Animation: pH-Dependent Electrophoresis and Microstate Composition of Glycine

Glycine's Ionization Microstates and pH-Dependent Electrophoresis Reload

Click to change pH.

Click to start animation.

;

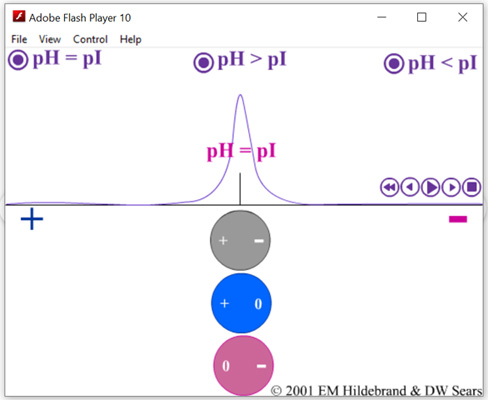
Example: The Isoelectric pH, or pI, of Glycine equals 6.1.

Assumptions: pKd(α-NH₃⁺) = 9.8 pKd(α-COOH) = 2.4

Electrophoresis Practice Quiz

4 Possible Microstates

Equilibrium Microstate Fractions at pH = 6.1

(+ -): NH₃⁺-CH₂-COO^-

At pH = 6.1, fraction = Ya(a-NH₃⁺) * Yd(a-COO^-) = 99.96%

(+ 0): NH₃⁺-CH₂-COOH

At pH = 6.1, fraction = Ya(a-NH₃⁺) * Ya(a-COOH) = 0.02%

(0 -): NH₂-CH₂-COO^-

At pH = 6.1, fraction = Yd(a-NH₂) * Yd(a-COO^-) = 0.02%

(0 0): NH₂-CH₂-COOH

At pH = 6.1, fraction = Yd(a-NH₂) * Ya(a-COOH) = 0.000004%

@ pI, net charge = 0 and Ya(α-NH₃⁺) = Yd(α-COO^-). Thus,Ya(α-NH₃⁺) = 1/(1+10^{pI-pKdn(NH3+)}) = Yd(α-COO^-) = 1/(1+10^{pKdn(COOH)-pI}).
(1+10^{pKdn(COOH)-pI}) = (1+10^{pI-pKdn(NH3+)}) or 10^{pKdn(COOH)-pI} = 10^{pI-pKdn(NH3+)} or pKdn(COOH)-pI = pI-pKdn(NH3+).
Thus, 2*pI = pKdn(NH3+) + pKdn(COOH), or pI = (1/2) * (pKdn(NH3+) + pKdn(COOH)).